MECÂNICA GRACELI GENERALIZADA - QUÂNTICA DIMENSIONAL TENSORIAL RELATIVISTA DE CAMPOS [1.317]

MECÂNICA GRACELI GENERALIZADA - QUÂNTICA TENSORIAL DIMENSIONAL RELATIVISTA DE CAMPOS.

MECÃNICA GRACELI GERAL - QTDRC.

$equação Graceli dimensional relativista tensorial quântica de campos$

$\psi ^{*}$

$[$ $\psi ^{*}$ $G$ * $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $T_{\mu \nu }$ $/$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $T_{\mu \nu }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ +

$+$ $G$ * $\psi ^{*}$ [ $\psi ^{*}$ ${\boldsymbol {\mu }}$ ] $\lambda$ ω ${\mathcal {T}}$ , $\sigma$ , $\psi$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ [x,t] ] =

//////

[

$\psi ^{*}$

$TeoriaInteraçãomediadorMagnitude relativaComportamentoFaixaCromodinâmicaForça nuclear forteGlúon10411/r71,4 × 10-15 mEletrodinâmicaForça eletromagnéticaFóton10391/r2infinitoFlavordinâmicaForça nuclear fracaBósons W e Z10291/r5 até 1/r710-18 mGeometrodinâmicaForça gravitacionalgráviton101/r2infinito$

Teoria	Interação	mediador	Magnitude relativa	Comportamento	Faixa
Cromodinâmica	Força nuclear forte	Glúon	1041	1/r7	1,4 × 10-15 m
Eletrodinâmica	Força eletromagnética	Fóton	1039	1/r2	infinito
Flavordinâmica	Força nuclear fraca	Bósons W e Z	1029	1/r5 até 1/r7	10-18 m
Geometrodinâmica	Força gravitacional	gráviton	10	1/r2	infinito

$G* = OPERADOR DE DIMENSÕES DE GRACELI.$

DIMENSÕES DE GRACELI SÃO TODA FORMA DE TENSORES, ESTRUTURAS, ENERGIAS, ACOPLAMENTOS, , INTERAÇÕES DE CAMPOS E ENERGIAS, DISTRIBUIÇÕES ELETRÔNICAS, ESTADOS FÍSICOS, ESTADOS QUÂNTICOS, ESTADOS FÍSICOS DE ENERGIAS DE GRACELI, E OUTROS.

/ $G$ * $\psi ^{*}$ [ $\psi ^{*}$ $T_{\mu \nu }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$

MECÂNICA GRACELI GENERALIZADA - QUÂNTICA TENSORIAL DIMENSIONAL RELATIVISTA DE INTERAÇÕES DE CAMPOS. EM ;

MECÂNICA GRACELI REPRESENTADA POR TRANSFORMADA.

dd = dd [G] = DERIVADA DE DIMENSÕES DE GRACELI.

- [ $G*$ $\hbar$ $.$ $\psi$

G { f [dd]} ´[d] $\psi ^{*}$ $\hbar$ $\psi$ $f [d] G*$ $T_{\mu \nu }$ $\psi$ $dd [G]$

O ESTADO QUÂNTICO DE GRACELI

- [ $G*$ $\hbar$ $.$ $\psi$ $\left|\psi \right\rangle ={\frac {1}{\sqrt {2}}}{\bigg (}\left|\uparrow \downarrow \right\rangle -\left|\downarrow \uparrow \right\rangle {\bigg )},$ ]

$G* = DIMENSÕES DE GRACELI TAMBÉM ESTÁ RELACIONADO COM INTERAÇÕES DE ENERGIAS, QUÂNTICAS, RELATIVÍSTICAS, , E INTERAÇÕES DE CAMPOS.$

o tensor energia-momento $T_{\mu \nu }$ é aquele de um campo eletromagnético,

/ $G$ * $\psi ^{*}$ [ $\psi ^{*}$ $T_{\mu \nu }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$

$G$ $E=mc^{2}$ ] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

$/$ $G$ $E=mc^{2}$ ] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

Na teoria quântica de campos, a Representação espectral de Källén-Lehmann fornece uma expressão geral para a função correlacional de dois pontos na mecânica quântica como uma soma de propagadores livres. Ela foi descoberta de forma independente por Gunnar Källén e Harry Lehmann. A representação pode ser escrita como

\Delta (p)=\int _{0}^{\infty }d\mu ^{2}\rho (\mu ^{2}){\frac {1}{p^{2}-\mu ^{2}+i\epsilon }}

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

onde $\rho (\mu ^{2})$ é a função de densidade espectral que deve ser definida positivamente, numa teoria de gauge, esta condição não pode ser garantida, mas uma representação espectral pode ser fornecida.^[1] Esta é uma técnica não perturbativa da teoria quântica de campos.

Definição

Para se obter uma representação espectral para o propagador de um campo $\Phi (x)$ , é necessário considerar um conjunto de estados $\{|n\rangle \}$ de forma que, a função correlacional pode ser escrita como

\langle 0|\Phi (x)\Phi ^{\dagger }(y)|0\rangle =\sum _{n}\langle 0|\Phi (x)|n\rangle \langle n\Phi ^{\dagger }(y)|0\rangle .

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

Agora utilizando o grupo de Poincaré do vácuo, obtêm-se

\langle 0|\Phi (x)\Phi ^{\dagger }(y)|0\rangle =\sum _{n}e^{-ip_{n}\cdot (x-y)}|\langle 0|\Phi (0)|n\rangle |^{2}.

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

Introduzindo-se a função de densidade espectral

\rho (p^{2})\theta (p_{0})(2\pi )^{-3}=\sum _{n}\delta ^{4}(p-p_{n})|\langle 0|\Phi (0)|n\rangle |^{2}.

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

Pode-se utilizar o facto que a função correlacional, sendo uma função de $p_{\mu }$ , apenas pode depender de $p^{2}$ . Além disto, todos os estados intermediários possuem $p^{2}\geq 0$ e $p_{0}>0$ . Logo percebe-se que a função de densidade espectral será real e positiva. Então pode-se escrever que

\langle 0|\Phi (x)\Phi ^{\dagger }(y)|0\rangle =\int {\frac {d^{4}p}{(2\pi )^{3}}}\int _{0}^{\infty }d\mu ^{2}e^{-ip\cdot (x-y)}\rho (\mu ^{2})\theta (p_{0})\delta (p^{2}-\mu ^{2})

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

e pode-se trocar a integral livremente, obtendo-se a expressão

\langle 0|\Phi (x)\Phi ^{\dagger }(y)|0\rangle =\int _{0}^{\infty }d\mu ^{2}\rho (\mu ^{2})\Delta '(x-y;\mu ^{2})

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

onde

\Delta '(x-y;\mu ^{2})=\int {\frac {d^{4}p}{(2\pi )^{3}}}e^{-ip\cdot (x-y)}\theta (p_{0})\delta (p^{2}-\mu ^{2})

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

Do teorema CPT sabe-se que uma expressão idêntica pode ser obtida para $\langle 0|\Phi ^{\dagger }(x)\Phi (y)|0\rangle$ e então conclui-se da expressão para o produto de campos cronologicamente ordenados

\langle 0|T\Phi (x)\Phi ^{\dagger }(y)|0\rangle =\int _{0}^{\infty }d\mu ^{2}\rho (\mu ^{2})\Delta (x-y;\mu ^{2})

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

onde

\Delta (p;\mu ^{2})={\frac {1}{p^{2}-\mu ^{2}+i\epsilon }}

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

é um propagador de partícula. Obtém-se a decomposição espectral.

Definição

\langle 0|\Phi (x)\Phi ^{\dagger }(y)|0\rangle =\sum _{n}\langle 0|\Phi (x)|n\rangle \langle n\Phi ^{\dagger }(y)|0\rangle .

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

Agora utilizando o grupo de Poincaré do vácuo, obtêm-se

\langle 0|\Phi (x)\Phi ^{\dagger }(y)|0\rangle =\sum _{n}e^{-ip_{n}\cdot (x-y)}|\langle 0|\Phi (0)|n\rangle |^{2}.

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

Introduzindo-se a função de densidade espectral

\rho (p^{2})\theta (p_{0})(2\pi )^{-3}=\sum _{n}\delta ^{4}(p-p_{n})|\langle 0|\Phi (0)|n\rangle |^{2}.

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

\langle 0|\Phi (x)\Phi ^{\dagger }(y)|0\rangle =\int {\frac {d^{4}p}{(2\pi )^{3}}}\int _{0}^{\infty }d\mu ^{2}e^{-ip\cdot (x-y)}\rho (\mu ^{2})\theta (p_{0})\delta (p^{2}-\mu ^{2})

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

e pode-se trocar a integral livremente, obtendo-se a expressão

\langle 0|\Phi (x)\Phi ^{\dagger }(y)|0\rangle =\int _{0}^{\infty }d\mu ^{2}\rho (\mu ^{2})\Delta '(x-y;\mu ^{2})

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

onde

\Delta '(x-y;\mu ^{2})=\int {\frac {d^{4}p}{(2\pi )^{3}}}e^{-ip\cdot (x-y)}\theta (p_{0})\delta (p^{2}-\mu ^{2})

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

\langle 0|T\Phi (x)\Phi ^{\dagger }(y)|0\rangle =\int _{0}^{\infty }d\mu ^{2}\rho (\mu ^{2})\Delta (x-y;\mu ^{2})

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

onde

\Delta (p;\mu ^{2})={\frac {1}{p^{2}-\mu ^{2}+i\epsilon }}

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

é um propagador de partícula. Obtém-se a decomposição espectral.

Teoria do campo Lagrangiana (de Lagrange) é um formalismo na teoria clássica de campos. É o campo análogo teórico da mecânica Lagrangiana. Mecânica lagrangiana é utilizado para partículas discretas, cada uma com um número finito de graus de liberdade. Teoria de campo Lagrangiana aplica-se ao contínuo e campos, que têm um número infinito de graus de liberdade.^[1]^[2]

Este artigo usa $\scriptstyle {\mathcal {L}}$ para a densidade Lagrangiana, e L para a Lagrangiana.

O formalismo da mecânica Lagrangiana foi generalizado ainda mais para lidar com teoria de campos. Na teoria de campos, a variável independente é substituída por um evento num espaço-tempo ( x , y , z , t ), ou, mais geralmente ainda, por um ponto s em uma variedade. As variáveis dependentes (q) são substituídas pelo valor de um campo em que um ponto no espaço-tempo φ (x, y, z, t) de modo que as equações de movimento são obtidas por meio de um princípio de ação, escrito como:

${\frac {\delta {\mathcal {S}}}{\delta \varphi _{i}}}=0,$

onde a ação, $\scriptstyle {\mathcal {S}},$ é um funcional das variáveis dependentes φ_i(s) com suas derivadas e com s em si mesmo

${\mathcal {S}}\left[\varphi _{i}\right]=\int {{\mathcal {L}}\left(\varphi _{i}(s),{\frac {\partial \varphi _{i}(s)}{\partial s^{\alpha }}},s^{\alpha }\right)\,\mathrm {d} ^{n}s}$

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

e onde s = { s^α} denota o conjunto de n variáveis independentes do sistemas, indexadas por α = 1, 2, 3,..., n.

Note-se que L é usado no caso de uma variável independente (t) e $\scriptstyle {\mathcal {L}}$ é utilizado no caso de múltiplas variáveis independentes (geralmente quatro: x, y, z, t).

Quebra espontânea de simetria é um processo pelo qual um sistema simétrico passa, de forma espontânea, para um estado não simétrico. Este tipo de processo, incomum na natureza física, é vital para a compreensão do modelo padrão das partículas fundamentais, que é um dos mais importantes ramos da física moderna.

Definição

Para que uma quebra espontânea de simetria ocorra, deve necessariamente haver um sistema no qual existam diversos estados subsequentes com iguais probabilidades de ocorrer. Este sistema, como um todo, então é tratado como um sistema simétrico. Entretanto apenas um dos estados subsequentes deve ocorrer e toda a probabilidade dos inúmeros estados diversos é reduzida a zero, já que não há mais simetria. Então, é dito que a simetria do sistema foi espontaneamente quebrada.

Definição formal

Quando uma teoria é dita simétrica com respeito à um grupo simétrico, mas afirma que um elemento deste grupo é distinto, então uma quebra espontânea de simetria ocorreu, ou seja, pela teoria, não é necessário que se identifique o elemento e sim apenas que haja um elemento distinto.

Importância no modelo padrão

Sem a quebra espontânea de simetria o modelo padrão prediz a existência de um determinado número de partículas. Entretanto, algumas destas partículas (os bosões W e Z, por exemplo) são preditos de não possuir massa, quando na realidade eles possuem massa. Esta era a maior falha do modelo até que o físico escocês Peter Higgs e outros propuseram, através do que ficou conhecido por mecanismo de Higgs, o uso da quebra espontânea de simetria para comportar massa nestas partículas. O mecanismo por sua vez prediz a existência de uma nova partícula, o bosão de Higgs. O bosão/bóson de Higgs foi detectado no LHC do CERN em Julho de 2012, com probabilidade maior que 5 sigmas de ser verdadeira tal identificação.

Uso na matemática

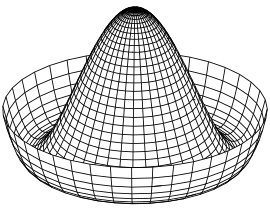
Na matemática o uso mais comum da quebra espontânea de simetria é pelo uso da Função de Lagrange, a qual essencialmente indica como um sistema irá se comportar por meio de termos potenciais

(1)\qquad {\mathcal {L}}=\partial ^{\mu }\phi \partial _{\mu }\phi -V(\phi ).

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

É neste termo potencial $V(\phi )$ que a ação da quebra de simetria ocorre. Como demonstra o gráfico do chapéu mexicano

(2)\qquad V(\phi )=-10|\phi |^{2}+|\phi |^{4}\,

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

Este termo potencial possui vários possíveis mínimos dados por

(3)\qquad \phi ={\sqrt {5}}e^{i\theta }

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

para qualquer real no intervalo $0<\theta <2\pi$ . Este sistema também possui um estado do vácuo quântico que corresponde ao $\phi =0$ , este estado possui um grupo unitário simétrico. Entretanto, uma vez que o sistema atinja um estado específico no vácuo (que corresponda a um valor para $\theta$ ) a simetria será espontaneamente quebrada.

Exemplos fora da Física

O fenômeno da quebra espontânea de simetria também é encontrado em Dinâmica de Tráfego de Veículos,^[1] sistemas difusivos,^[2] econômicos^[3] e sociais.^[4]

Search This Blog

MECÂNICA GRACELI GENERALIZADA - QUÂNTICA DIMENSIONAL TENSORIAL RELATIVISTA DE CAMPOS [1.317]

Definição

Definição

Definição

Definição formal

Importância no modelo padrão

Uso na matemática

Exemplos fora da Física

Comments

Post a Comment

Popular posts from this blog