MECÂNICA GRACELI GENERALIZADA - QUÂNTICA DIMENSIONAL TENSORIAL RELATIVISTA DE CAMPOS [1.317]

MECÂNICA GRACELI GENERALIZADA - QUÂNTICA TENSORIAL DIMENSIONAL RELATIVISTA DE CAMPOS.

MECÃNICA GRACELI GERAL - QTDRC.

$equação Graceli dimensional relativista tensorial quântica de campos$

$\psi ^{*}$

$[$ $\psi ^{*}$ $G$ * $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $T_{\mu \nu }$ $/$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $T_{\mu \nu }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ +

$+$ $G$ * $\psi ^{*}$ [ $\psi ^{*}$ ${\boldsymbol {\mu }}$ ] $\lambda$ ω ${\mathcal {T}}$ , $\sigma$ , $\psi$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ [x,t] ] =

//////

[

$\psi ^{*}$

$TeoriaInteraçãomediadorMagnitude relativaComportamentoFaixaCromodinâmicaForça nuclear forteGlúon10411/r71,4 × 10-15 mEletrodinâmicaForça eletromagnéticaFóton10391/r2infinitoFlavordinâmicaForça nuclear fracaBósons W e Z10291/r5 até 1/r710-18 mGeometrodinâmicaForça gravitacionalgráviton101/r2infinito$

Teoria	Interação	mediador	Magnitude relativa	Comportamento	Faixa
Cromodinâmica	Força nuclear forte	Glúon	1041	1/r7	1,4 × 10-15 m
Eletrodinâmica	Força eletromagnética	Fóton	1039	1/r2	infinito
Flavordinâmica	Força nuclear fraca	Bósons W e Z	1029	1/r5 até 1/r7	10-18 m
Geometrodinâmica	Força gravitacional	gráviton	10	1/r2	infinito

$G* = OPERADOR DE DIMENSÕES DE GRACELI.$

DIMENSÕES DE GRACELI SÃO TODA FORMA DE TENSORES, ESTRUTURAS, ENERGIAS, ACOPLAMENTOS, , INTERAÇÕES DE CAMPOS E ENERGIAS, DISTRIBUIÇÕES ELETRÔNICAS, ESTADOS FÍSICOS, ESTADOS QUÂNTICOS, ESTADOS FÍSICOS DE ENERGIAS DE GRACELI, E OUTROS.

/ $G$ * $\psi ^{*}$ [ $\psi ^{*}$ $T_{\mu \nu }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$

MECÂNICA GRACELI GENERALIZADA - QUÂNTICA TENSORIAL DIMENSIONAL RELATIVISTA DE INTERAÇÕES DE CAMPOS. EM ;

MECÂNICA GRACELI REPRESENTADA POR TRANSFORMADA.

dd = dd [G] = DERIVADA DE DIMENSÕES DE GRACELI.

- [ $G*$ $\hbar$ $.$ $\psi$

G { f [dd]} ´[d] $\psi ^{*}$ $\hbar$ $\psi$ $f [d] G*$ $T_{\mu \nu }$ $\psi$ $dd [G]$

O ESTADO QUÂNTICO DE GRACELI

- [ $G*$ $\hbar$ $.$ $\psi$ $\left|\psi \right\rangle ={\frac {1}{\sqrt {2}}}{\bigg (}\left|\uparrow \downarrow \right\rangle -\left|\downarrow \uparrow \right\rangle {\bigg )},$ ]

$G* = DIMENSÕES DE GRACELI TAMBÉM ESTÁ RELACIONADO COM INTERAÇÕES DE ENERGIAS, QUÂNTICAS, RELATIVÍSTICAS, , E INTERAÇÕES DE CAMPOS.$

o tensor energia-momento $T_{\mu \nu }$ é aquele de um campo eletromagnético,

/ $G$ * $\psi ^{*}$ [ $\psi ^{*}$ $T_{\mu \nu }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$

$G$ $E=mc^{2}$ ] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

$/$ $G$ $E=mc^{2}$ ] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

Quebra espontânea de simetria é um processo pelo qual um sistema simétrico passa, de forma espontânea, para um estado não simétrico. Este tipo de processo, incomum na natureza física, é vital para a compreensão do modelo padrão das partículas fundamentais, que é um dos mais importantes ramos da física moderna.

Definição

Para que uma quebra espontânea de simetria ocorra, deve necessariamente haver um sistema no qual existam diversos estados subsequentes com iguais probabilidades de ocorrer. Este sistema, como um todo, então é tratado como um sistema simétrico. Entretanto apenas um dos estados subsequentes deve ocorrer e toda a probabilidade dos inúmeros estados diversos é reduzida a zero, já que não há mais simetria. Então, é dito que a simetria do sistema foi espontaneamente quebrada.

Definição formal

Quando uma teoria é dita simétrica com respeito à um grupo simétrico, mas afirma que um elemento deste grupo é distinto, então uma quebra espontânea de simetria ocorreu, ou seja, pela teoria, não é necessário que se identifique o elemento e sim apenas que haja um elemento distinto.

Importância no modelo padrão

Sem a quebra espontânea de simetria o modelo padrão prediz a existência de um determinado número de partículas. Entretanto, algumas destas partículas (os bosões W e Z, por exemplo) são preditos de não possuir massa, quando na realidade eles possuem massa. Esta era a maior falha do modelo até que o físico escocês Peter Higgs e outros propuseram, através do que ficou conhecido por mecanismo de Higgs, o uso da quebra espontânea de simetria para comportar massa nestas partículas. O mecanismo por sua vez prediz a existência de uma nova partícula, o bosão de Higgs. O bosão/bóson de Higgs foi detectado no LHC do CERN em Julho de 2012, com probabilidade maior que 5 sigmas de ser verdadeira tal identificação.

Uso na matemática

Na matemática o uso mais comum da quebra espontânea de simetria é pelo uso da Função de Lagrange, a qual essencialmente indica como um sistema irá se comportar por meio de termos potenciais

(1)\qquad {\mathcal {L}}=\partial ^{\mu }\phi \partial _{\mu }\phi -V(\phi ).

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

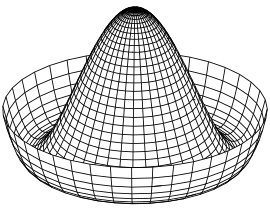
É neste termo potencial $V(\phi )$ que a ação da quebra de simetria ocorre. Como demonstra o gráfico do chapéu mexicano

(2)\qquad V(\phi )=-10|\phi |^{2}+|\phi |^{4}\,

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

Este termo potencial possui vários possíveis mínimos dados por

(3)\qquad \phi ={\sqrt {5}}e^{i\theta }

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

para qualquer real no intervalo $0<\theta <2\pi$ . Este sistema também possui um estado do vácuo quântico que corresponde ao $\phi =0$ , este estado possui um grupo unitário simétrico. Entretanto, uma vez que o sistema atinja um estado específico no vácuo (que corresponda a um valor para $\theta$ ) a simetria será espontaneamente quebrada.

Para um sistema físico composto por partículas de spin zero, existe um potencial de Coulomb blindado que é conhecido como potencial de Yukawa. Tal pontencial é da forma

$V\left(r\right)=-{\frac {g_{s}}{4\pi r}}e^{-{\frac {mrc}{\hbar }}}$

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

e que é, claramente, um potencial do tipo central. Na equação acima, $g_{s}$ é uma constante (positiva) de acoplamento que configura a intensidade da força efetiva, $�$ é a massa da partícula afetada pelo potencial, $�$ é a velocidade da luz e $\hbar$ a constante de Planck. Naturalmente, podemos mostrar que o potencial $V(r)$ está associada a uma força sempre atrativa.

Em mecânica quântica, um propagador é uma função ou distribuição que descreve a amplitude da probabilidade de uma partícula se mover de uma posição para outra. Tecnicamente, é a função de Green para a equação do movimento.

Definição

Partícula não-relativística

O propagador $K(x,t;x',t')$ é uma função ou distribuição que verifica a seguinte equação:

\left(\mathrm {i} \hbar {\frac {\partial }{\partial t}}-H\right)K(\mathbf {x} ,t;\mathbf {x} ',t')=\delta (x-x')\delta (t-t')

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

Aqui $�$ é o hamiltoniano e $\delta$ é a distribuição dirac.

Por exemplo, considere uma partícula não relativística livre. O propagador, portanto, verifica:

\left(\mathrm {i} \hbar {\frac {\partial }{\partial t}}-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}\right)K(\mathbf {x} ,t;\mathbf {x} ',t')=\delta (x-x')\delta (t-t')

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

Para resolver isso, converta em momento- e espaço de frequência :

(\hbar \omega -\hbar ^{2}p^{2}/2m)K(\mathbf {p} ,\omega )=1

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

Seguindo-se que:

K(\mathbf {p} ,\omega )={\frac {1}{\hbar \omega -\hbar ^{2}p^{2}/2m}}

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

Converta de volta para posição e espaço-tempo:

K(\mathbf {x} ,t;\mathbf {x} ',t')=\int {\frac {\operatorname {d} ^{3}\!\mathbf {k} \;\operatorname {d} \!\omega }{(2\pi )^{4}}}\exp(\mathrm {i} (\mathbf {k} \cdot (\mathbf {x} -\mathbf {x} ')-\omega (t-t')))K(\mathbf {p} ,\omega )

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

A integral é ambígua, porque tem um pólo em

\omega =\hbar p^{2}/2m

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

Deve-se desambiguar a integral adicionando um infinitesimal, mas existem dois sinais possíveis (Por isso o propagador não é único). Ao adicionar um infinitesimal pode-se calcular:

K_{\pm }(\mathbf {x} ,t;\mathbf {x} ',t')

=\int {\frac {\operatorname {d} ^{3}\!\mathbf {k} \;\operatorname {d} \!\omega }{(2\pi )^{4}}}\exp(\mathrm {i} (\mathbf {k} \cdot (\mathbf {x} -\mathbf {x} ')-\omega (t-t'))){\frac {1}{\hbar \omega \pm \mathrm {i} \epsilon -\hbar ^{2}p^{2}/2m}}

=\mp {\frac {\mathrm {i} }{\hbar }}\theta (\pm t\mp t')\left({\frac {m}{2\pi \mathrm {i} \hbar (t-t')}}\right)^{3/2}\exp \left({\frac {\mathrm {i} m}{2\hbar (t-t')}}(\mathbf {x} -\mathbf {x} ')^{2}\right)

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

Onde:

\theta (x)={\begin{cases}1&{\text{se }}x>0\\0&{\text{se }}x<0\end{cases}}

Representa a função de Heaviside. A função $K_{+}$ chamada de propagador passado (retarded em inglês), porque $K_{+}(\mathbf {x} ,t;\mathbf {x} ',t')$ é diferente de zero apenas se $t>t'$ . Enquanto isso, a função $K_{-}$ é chamada de propagador futuro (advanced em inglês), porque $K_{-}(\mathbf {x} ,t;\mathbf {x} ',t')$ é diferente de zero apenas se $t<t'$ .

Partícula relativística

Usamos uma convenção de sinalização $+---$ para a métrica que, $x\cdot y=x^{0}y^{0}-\mathbf {x} \cdot \mathbf {y}$ .

Uma partícula escalar relativística verifica a equação de Klein-Gordon . Daí o propagador $K(x,y)$ de uma partícula escalar relativística é definido como a função de Green da equação de Klein-Gordon. Eis:

(\partial ^{2}+m^{2})K(x,y)=-\delta (x-y)

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

Para resolver, converte-se em momento linear:

(p^{2}-m^{2})K(p)=1

Então:

K(p)={\frac {1}{p^{2}-m^{2}}}

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

Converte-se de volta para o espaço de posição:

K(x,y)=\int {\frac {\operatorname {d} ^{4}\!p}{(2\pi )^{4}}}{\frac {1}{p^{2}-m^{2}}}

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

A integral é ambígua porque tem dois pólos em:

p^{0}=\pm (\mathbf {p} ^{2}+m^{2})

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

Deve-se desambiguar a integral adicionando um infinitesimal. De acordo com a teoria da integral curvilínea, podemos subir ou descer em cada pólo. Portanto, existem quatro métodos diferentes para eliminar a ambiguidade da integral; o propagador não é único. Se subirmos pelos dois pólos, o passado (em inglês retarded) será encontrado:

K_{\mathrm {R} }(x,y)=\int {\frac {\operatorname {d} ^{4}\!p}{(2\pi )^{4}}}{\frac {1}{(p_{0}+\mathrm {i} \epsilon )^{2}-\mathbf {p} ^{2}-m^{2}}}

={\begin{cases}\left(-\delta (s)+m\operatorname {J} _{1}(m{\sqrt {s}})/2{\sqrt {s}}\right)/2\pi &{\text{se }}x^{0}>y^{0}{\text{ kaj }}s\geq 0\\0&{\text{alie}},\end{cases}}

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

Onde $\operatorname {J} _{1}$ representa a função de Bessel de primeiro tipo e $s=(x-y)^{2}$ . Se descermos em ambos os pólos, o propagador futuro (advanced) será encontrado:

K_{\mathrm {A} }(x,y)=\int {\frac {\operatorname {d} ^{4}\!p}{(2\pi )^{4}}}{\frac {1}{(p_{0}-\mathrm {i} \epsilon )^{2}-\mathbf {p} ^{2}-m^{2}}}

={\begin{cases}\left(-\delta (s)+m\operatorname {J} _{1}(m{\sqrt {s}})/2{\sqrt {s}}\right)/2\pi &{\text{se }}x^{0}<y^{0}{\text{ kaj }}s\geq 0\\0&{\text{alie}}.\end{cases}}

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

Se descermos pelo pólo esquerdo (em $p^{0}=-{\sqrt {\mathbf {p} ^{2}+m^{2}}}$ e para cima através do pólo direito (em $p^{0}=+{\sqrt {\mathbf {p} ^{2}+m^{2}}}$ ), O propagador de Feynman será encontrado:

K_{\mathrm {F} }(x,y)=\int {\frac {\operatorname {d} ^{4}\!p}{(2\pi )^{4}}}{\frac {\exp(-\mathrm {i} p\cdot (x-y))}{p^{2}-m^{2}+\mathrm {i} \epsilon }}

={\begin{cases}\left(-\delta (s)+m\operatorname {H} _{1}^{(1)}(m{\sqrt {s}})/2{\sqrt {s}}\right)/2\pi &{\text{se }}s\geq 0\\-\mathrm {i} m\operatorname {K} _{1}(m{\sqrt {-s}})/(4\pi ^{2}{\sqrt {-s}})&{\text{se }}s<0,\end{cases}}

$/$ $G$

E=mc^{2}

] $-i\hbar {\frac {\partial }{\partial x_{n}}}$

Onde $\operatorname {H} _{1}^{(1)}$ representa a função de Hankel de primeiro tipo e $\operatorname {K} _{1}$ significa a função modificada de Bessel de segundo tipo. Se subirmos pelo pólo esquerdo e descermos pelo pólo direito, o propagador de Dyson encontrar-se-á: